The Conjugate Gradient method is one method that, in theory, converges to an exact solution in a limited number of steps. The Gradient working equation can be expressed for the pressure network system of equations as:

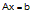
where:

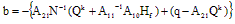
The structure of the system matrix A at the point of solution is:

and it can be seen that the nature of the topological matrix components yield a total working matrix A that is:

• Symmetric
• Positive definite
• Stieltjes type.

Because of the symmetry, the number of non-zero elements to be retained in the matrix equals the number of nodes plus the number of links. This results in a low density, highly sparse matrix form. It follows that an iterative solution scheme would be preferred over direct matrix inversion in order to avoid matrix fill-in, which serves to increase the computational effort.

Because the system is symmetric and positive definite, a Cholesky factorization can be performed to give:

where L is lower triangular with positive diagonal elements. Making the Cholesky factorization allows the system to be solved in two steps:

The use of this approach over more general sparse matrix solvers that implement traditional Gaussian elimination methods without consideration to matrix symmetry is preferred since performance gains are considerable. The algorithm utilized in this software solves the system of equations using a variant of Cholesky’s method which has been optimized to reduce fill-in of the factorization matrix, thus minimizing storage and reducing overall computational effort.